Appendix N — Assignment 9

Author

phonchi

Published

May 28, 2023

N.1 (1) Which of the following statement is False?

  1. We can evaluate the values of special constants, like \(e\), \(\pi\), and \(\infty\) using SymPy.

  2. You can express one symbol in terms of another and perform substitutions accordingly, using the subs() method. For instance, you can substitute \(\cos(x)\) with \(\sin(x+\pi/2)\) by calling subs({sp.cos(x):sp.sin(x+sp.pi/2)}).

  3. nsolve() function is a numerical version of the solve() function. Therefore, if solve() function fails to find a solution, nsolve() function will also fail to find a solution.

  4. The lambdify() function in SymPy converts SymPy expressions into equivalent Python functions, enabling them to be computed numerically.

Ans: Double click to answer the question

  1. If solve() fails to find a solution, it doesn’t mean nsolve() will also fail. They use different methods and can handle different types of equations.

N.2 (2) Which of the following function can be use to display the expression in the reverse order, so that the terms of an expression are arranged according to the powers of x, in ascending order?

  1. init_printing()

  2. evalf()

  3. simplify()

  4. lambdify()

Ans: Double click to answer the question

N.3 (3) Which of the following statement is False?

  1. By default, the direction from which the limit is computed is negative in SymPy, unless the point of computation is positive or negative infinity.

  2. When constructing a matrix in SymPy, the approach is quite similar to that of NumPy. You provide a list of lists, where each inner list is a row of the matrix.

  3. By default, the solve() function will return the solutions in a list.

  4. In sympy, you can expand a trigonometric expression by setting trig=True in the expand() function.

Ans: Double click to answer the question

  1. By default, the direction from which the limit is computed is positive in SymPy.

N.4 (4) Which of the following operation will return the evaluation results rather than an unevaluated object?

  1. sp.Limit(1/x, x, -sp.oo)

  2. sp.Derivative(1/x, x)

  3. sp.diff(x**2, x)

  4. sp.Integral(x**2)

Ans: Double click to answer the question

N.5 (5) Which of the following function can be used to evaluate an expression to a floating-point number?

  1. doit()

  2. simplify()

  3. lambdify()

  4. evalf()

Ans: Double click to answer the question

N.6 (6) Consider the following two equations:

\[ \begin{align} x + y + z &= 6 \\ 2x + 3y + z &= 12 \\ 3x - 2y + z &=2 \end{align} \]

Try to find the pair of values (x, y) that satisfies both equations using SymPy. After that, substitute the values of x and y into the original equations to verify that the solutions are correct using SymPy.

%pip install sympy --upgrade
Collecting sympy
  Downloading sympy-1.12-py3-none-any.whl (5.7 MB)
Requirement already satisfied, skipping upgrade: mpmath>=0.19 in c:\users\phonchi\anaconda3\lib\site-packages (from sympy) (1.1.0)
Installing collected packages: sympy
  Attempting uninstall: sympy
    Found existing installation: sympy 1.6.1
    Uninstalling sympy-1.6.1:
      Successfully uninstalled sympy-1.6.1
Successfully installed sympy-1.12
Note: you may need to restart the kernel to use updated packages.
import sympy as sp
x = sp.Symbol('x')
y = sp.Symbol('y')
z = sp.Symbol('z')
expr1 = x + y +z - 6
expr2 = 2*x + 3*y +z - 12
expr3 = 3*x - 2*y + z - 2

sp.solve((expr1, expr2, expr3), dict=True)
[{x: 10/7, y: 16/7, z: 16/7}]
sol = sp.solve((expr1, expr2, expr3), dict=True)
expr1.subs({x:sol[0][x], y:sol[0][y], z:sol[0][z]}), expr2.subs({x:sol[0][x], y:sol[0][y], z:sol[0][z]}), expr3.subs({x:sol[0][x], y:sol[0][y], z:sol[0][z]})
(0, 0, 0)

N.7 (7) Factoring the following polynomial, and finding its roots using SymPy:

\[x^4-6x^3+x^2+24x+16\]

x = sp.Symbol('x')
p1 = x**4 - 6*x**3+x**2+24*x+16
sp.factor(p1)

\(\displaystyle \left(x - 4\right)^{2} \left(x + 1\right)^{2}\)

sp.solve(p1, dict=True)
[{x: -1}, {x: 4}]

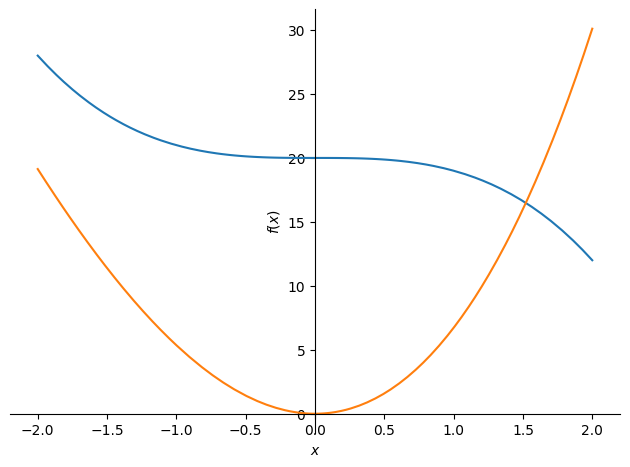
N.8 (8) Find all the intersection points between \(f(x)=20-x^3\) and \(g(x)=6x^2 \times 1.12^x\) using SymPy by first plotting the function and using the graph to narrow down the range of the intersection points. Then, use nsolve() function to find the intersection points. Your results should be the coordinate values in numerical format.

Hint: You may find solve() and nroots() can not be used to solve this problem. In addition, you may need to zoom in around 0 to find all the possible intersection points.

x = sp.Symbol('x')
sp.plot(20-x**3, 6*x**2*1.12**x, (x, -2, 2));

expr1 = 20-x**3 - 6*x**2*1.12**x
eq1 = 20-x**3
eq2 = 6*x**2*1.12**x
xx = sp.nsolve(expr1, 1)
xx, eq1.subs(x, xx), eq2.subs(x, xx)
(1.52065140948474, 16.4836750153385, 16.4836750153385)

N.9 (9) Try to evaluate the expression \(\log{3}+e\) to 20 precision (significant digits) using SymPy.

(sp.log(3)+sp.E).evalf(20)

\(\displaystyle 3.8168941171271549268\)

N.10 (10) Try to solve the following problems using SymPy:

Simplify the following expression: \(\tan(x)\times \cos(3x) \times \sin(x)\) so that the final results only contains sin(x) and its power term (\(\sin^n(x)\)).

Hint: You can use simplify() and expand() functions to simplify the expression. You may find trig=True option in expand() function useful.

x = sp.Symbol('x')
exp = sp.tan(x)*sp.cos(3*x)*sp.sin(x)
exp2 = sp.simplify(exp.expand(trig=True))
exp2

\(\displaystyle - 4 \sin^{4}{\left(x \right)} + \sin^{2}{\left(x \right)}\)